INTRODUCTIONThroughout the past years, the area of Otorhinolaryngology has employed new techniques to assess laryngeal conditions. Since the use of Gancia mirror, to reflect the laryngeal image, the technology advances have been quickly incorporated into the clinical practice of the specialist, reaching a level of sophisticated recording in video of phonation using videolaryngoscopes, stroboscopes and real time analysis of vocal fold vibration patterns using computers.
Magnetic resonance imaging (Story et al., 1996; Story et al. 1998) enabled the evaluation of laryngeal structures concerning the anatomic disposition and the organic constitution. However, such technique only enables static analysis since the equipment does not allow the recording of sequence of images during phonation in the interval required for real time analysis.
By fixing an acceleration meter on the laryngeal region of the patients (Hertegard and Gauffin, 1995; Orlikoff, 1995) it is possible to record the vocal fold vibration during phonation. The glottal signal (coming from the vibration) is determined as such as its temporal and spectral properties are assessed and finally associated with the anatomic and physiological characteristics of the larynx. Considering that the vibration signal of vocal folds is attenuated by the neck walls (filtering the high frequency components of glottal signal), magnetic devices (Titze et al., 2000) were designed to obtain the glottal signal immune to this attenuation.
Currently, the acoustic voice analysis (Rosa et al., 2000) has allowed otorhinolaryngologists to assess the larynx by analyzing the voice signal pattern produced by the patient. Through a set of mathematical techniques for quantification of jitter (perturbation of fundamental frequency in the voice signal), shimmer (perturbation of fundamental amplitude) and noise, the specialist determines quantitatively the quality of vocalization of the patient and, indirectly, the physiological characteristics of the larynx.
The combination of these techniques enables the specialist to have qualitative and quantitative assessments that are more precise about the pathological condition of patients' larynxes.
An alternative way to objectively assess the larynx is to represent it through a biomechanical model in which the elements are directly related to the viscoelastic and geometric properties of muscle tissues of the larynx and the physical characteristics of the air. Such approach enables that glottal signal and voice be synthesized and compared to equivalent patient's signals. Thus, laryngeal modeling enables more objective studies concerning dynamics of the phonation process.
The literature has presented simplified models of larynx employing elements such as the masses attached to the rigid walls by springs and shock absorbers. The main model is the two-mass model by Ishizaka and Flanagan (1972), on which various improvements have been made.
The imposed simplifications, such as on laryngeal symmetry, simplified mathematical structures for calculation of aerodynamic outflow, and limited number of structures for the biomechanical representation of the vocal folds did not allow precise assessment of how the disease affects the larynx and its vibration. If we consider affections such as nodules and polyps that affect specific portions of the vocal folds, such models should evolve by incorporating more anatomical and physiological laryngeal characteristics.
Based on this, we propose a complete three-dimensional model of the larynx. It involves the definition of viscoelastic properties of muscle tissue structures, the arrangement of fibers, and three-dimensional geometry of the larynx. In addition, to develop mathematical methods to determine the dynamic behavior of air outflow and muscle tissues.
Once defined, this three-dimensional model enables the larynx to be virtually assessed. To assess tissue movements from the subglottal cavity (something impossible for conventional laryngoscopy) during phonation, distribution of pressures over the vocal fold walls, air flow in the glottal cavity, the forces involved in the collision between the vocal folds, are all examples of the analyses that can be made.
Through a process named analysis-by-synthesis, the specialist can synthesize the glottal signals and the voice and compare them to those produced by the patients. It allows validation of diagnosis by the specialist since the model is precisely reproducing the physiological characteristics of the patient's larynx. Assessments of vibration pattern of adjacent tissues of a cyst and the exact amount of air escaping through spindle chinks become feasible.
Subsequently to diagnosis, the specialist can virtually operate the patient, checking effectiveness of surgical interventions before the actual performance. An example is teflon injection (or any other material) in cases of vocal fold paralysis to provide glottal closure. Known the viscoelastic characteristics of the material, the specialist can use the three-dimensional model to check what is the effect of the surgical intervention in the vocal fold vibration, assessing the most appropriate position for the graft and the necessary amount of material to provide improvement of phonation conditions of the patient.
The purpose of the present study was to introduce a new tool and to demonstrate that it enables otorhinolaryngologists to perform a more objective assessment of the larynx in their patients using information that was previously impossible to be obtained. Moreover, the virtual treatment of patients is a technology that enables acceleration of patients' recovery after the surgery, since it allows the specialist to test ideas before putting them into action.
It is important to point out that despite the evident futuristic appeal of the approach, it is feasible and places the clinical practice of the specialist in another level, in which more sophisticated knowledge about the organic laryngeal structure (its viscoelastic properties, for example) is required.
Description of the three-dimensional model
The first step in describing the three-dimensional model of the larynx is its geometrical definition. It is made by dividing the larynx in hyper- elliptical sections (we can also use the technique of millimeter sections to determine laryngeal geometry). This set of geometrical entities allows computerized reconstruction of the larynx. In addition, we can make use of solid modeling techniques to refine the digital laryngeal surface. Figure 1 shows the segment of a digital larynx.
Based on the definition of the surfaces that define the laryngeal region to be analyzed, a computer algorithm divides the space involved by such surfaces in various tetrahedrons. This set of geometrical elements is named mesh. There are two different meshes: one of them describes the organic laryngeal structures (muscle tissues and cartilages), whereas the other defines the space through which the air flows. It occurs because it is necessary to determine the speeds of air pressure through the larynx, and it implies the need to specify the geometrical space.
The equation of solid dynamics is used to describe mathematically the displacements of the laryngeal mesh, whereas the equations of Navier-Stokes are used to calculate the speeds and pressures of the flow mesh. These equations (partial differential) describe the physical phenomenon that occurs in the larynx during phonation.
To represent flow, the equations of Navier-Stokes (Equation 1) are directly solved in the laryngeal cavity, differently from Ishizaka and Flanagan (1972) who adopted a simplification to determine the decrease in transglottal pressure and air flow in the larynx.
where Uf is the speed vector, P is the aerodynamic pressure, f and f are density and air viscosity, respectively (considering f =0.000123 g/cm3 and f =0.000179 dina.s/cm2).
The excitation of airflow is caused by different pressures. The lung pressure during phonation is about 8 cmH20 whereas the epiglottis pressure is close to the atmospheric pressure (zero cmH20) for open vowels. In addition, we considered that laryngeal walls air pressure is null. Such characteristics - contour conditions - enable the calculation of speeds and pressures throughout the flow mesh.
The airflow is easily described in the equations already mentioned; on the other hand, laryngeal tissues require special treatment. Considering the orientation of fibers along the vocal folds (longitudinal), a transversally isotropic linear model is employed. It occurs because laryngeal fibers are more rigid in the longitudinal direction (anterior-posterior) than in the vocal fold transversal plan. To facilitate the mathematical representation, a linear model is adopted.
In addition, differentiation of tissues in the vocal fold is also considered. Following the histology classification of Hirano (1975), the vocal folds present three types of tissue: the cover (involving epithelial tissue and the superficial layer of lamina propria), ligament (intermediate and profound layers of the lamina propria) and body (vocal muscle). In the model, each of these tissues is characterized by different elastic and viscosity properties. The determination of elastic properties of tissues is made by tissue distension trials (Chan and Titze, 1999; Alipour-Haghighi and Titze, 1991, Tran et al., 1993), whereas viscosity is defined based on human tissue characteristics (Titze and Talkin, 1979). Note that viscoelastic characterization was made based on mechanical trials of the larynx in cadavers or in vivo (especially the transversal Young E' model, according to the technique by Tran et al. [1993]).
Considering these histology characteristics of the larynx, Table 1 presents the elastic constants that define the three types of transversally isotropic linear model. Note that the transversal Young E model has amplitude proportion to tissue depth, as commented by Titze and Talkin (1979). According to them, body, ligament and cover rigidity can be proportional to the factors 10:4:2. The same authors stated that the longitudinal shear constant ' should be elevated to the ligament so as to represent its role in the connection between cover and body. Berry and Titze (1996) conducted a study assessing the influence of the pair E/ ' in the vibration of vocal folds, considering them as a solid compact. The longitudinal Young E' module is the easiest to obtain. A standardized value was defined for the whole larynx, admitting that the structure has a similar behavior when pulled, according to the analysis made by Alipour-Haghighi and Titze (1991).
Viscosity is the most difficult element to be assessed. According to Titze and Talkin (1979), 150 Poise was adopted for body tissue because of the similarity with other human tissues from where the value was estimated. However, for cover and ligament, this value was too high to sustain the oscillation. It would be the result of the viscous magnitude that absorbed the fiber movements. Berry and Titze (1996) also used low values for this constant in their simulation, showing the need for low viscosity for the cover, so that the vibration can be sustained.
Finally, Poisson constants ( and ') were defined as the way to keep quasi-incompressible muscle tissues. Titze and Talkin (1979) emphasized that such characteristic should be maintained to ensure that the vibration of the mathematical model be compatible with the vibration of the real larynx. Since a model of linear tension-deformation was used, these constants should mathematically validate the thermodynamic limit of the structure, that is,
(2)
Equation 2 only informs that the described muscle system does not produce energy, but only keeps it (signal of equality) or dissipates it (signal of subtraction).
As the contour condition for the resolution of the laryngeal equations, we fixed the larynx by the external surface - null displacement in the knots that comprise the surface. The so-called internal surface - in contact with the flow - is excited by aerodynamic pressure, which varies in time according to mesh movement.
The method of finite elements (Bathe, 1996) is used to solve laryngeal and flow equations for its easiness to work with non-structured meshes (where tetrahedrons geometrically differ one from the other). It is important because the larynx moves and thus it requires automatic mapping of its new geometrical characteristics every minute of the analyzed time. It is important to point out that there is not an analytical solution (exact) for the listed equations. Therefore, the used method enables numerical resolution of the equations. The higher the number of tetrahedrons (becoming smaller), the more points (or knots) are employed to determine the spatial movements of the larynx and speeds and pressures of flow, and the greater is the precision in solution. Thus, the solution of these equations gets progressively close to the exact solution. However, computer requirements to calculate the variable existing quantity become exponential. Thus, a good simulation requires commitment with precision and computer load.
In addition, vocal folds collide during phonation, restricting the air passage through the glottis. To represent this physical phenomenon, collision (or contact) equations are derived according to the techniques commonly found in mechanical models (Bathe, 1996). The main idea is to have sufficient force to prevent penetration of bodies one into the others. Considering the problem of laryngeal simulation, when both folds suffer coaptation, action and reaction forces are produced over the walls in order to restrict the movement.
The basic algorithm that describes the laryngeal simulation process is:
1. collection of aerodynamic pressures over the laryngeal walls;
2. calculation of the laryngeal movement when it suffers the action of aerodynamic pressures (considering possible collisions);
3. update of laryngeal mesh;
4. update of flow mesh;
5. calculation of the aerodynamic pressures and speeds of flow.
Note that the process is interactive. It means that at every instant, all equations are calculated sequentially. The coupling among both the physical systems (larynx and airflow) is based on the update of the mesh (new mesh, new airflow pattern) and aerodynamic pressures (laryngeal compression). The time intervals between the interactive cycles should be well defined according to the existing mathematical restrictions in the laryngeal and airflow equations and with the degree of temporal detailing that we wish to have. The conducted trials required time intervals of 0.0003 seconds.
It is a large-scale simulation since the set of 15,000 equations for flow and 15,000 equations for the larynx are solved in each iteration. It means that the movement of 5,000 mesh points are mapped and calculated each second of time. For flow purposes, the speed and pressure are calculated in 5,000 points in the laryngeal cavity. Thus, each segment (some below 1 millimeter) has its anatomy and physiology represented and simulated in the model.
RESULTSIn order to demonstrate the operation of the proposed model, a normal larynx was simulated. The geometry was obtained based on in vivo measures and magnetic resonance imaging. To characterize muscle tissues, we used viscoelasticity measures of fibers obtained from the literature. To excite the three-dimensional model, air pressure from the lungs (8kdian/cm2) and epiglottis (zero dina/cm2) were defined, creating aerodynamic conditions to sustain the flow through the larynx. Figure 2 shows the glottal signal, which corresponds to the flow measures as glottic output.
First, we noticed that initial oscillations were irregular, characterizing a transient pattern. In these initial instants, cover tissues start to move without, however, causing collision between the vocal folds.
The collisions between vocal folds can only be initiated after 20ms, despite the fact that the interval in which they remained together was very small. It occurs because both vocal folds are acquiring kinetic energy, beating the resistance of aerodynamic and viscoelastic forces of the tissue (the latter pertinent to the laryngeal tissue). It is interesting to keep in mind that when tissue viscosity (especially of the cover) is excessive, kinetic energy is not enough to beat the tissue resistance to movement.
As of 60ms, the larynx moves periodically, leaving a transient status of vibration. Note that after this movement, the glottal signal reaches its maximum amplitude. Numerically, the glottal signal obtained has 164Hz with an opening ratio equal to 0.6347 (that is, in 63.47% of the complete time cycle, the glottis is abducted and in the remaining cycle, it is adducted).
An interesting phenomenon is observed in simulations: incomplete closure of glottis. There are situations in which the viscoelastic conditions of tissues and laryngeal anatomy prevent the complete adduction of the glottis. It causes air leak with extremely reduced flow. In pathological situations, the onset of spindle chink in the anterior commissure causes excessive air leak that affects the patients' voice.
This incomplete glottic closure (as shown in Figure 3) is caused by the uneven distribution of aerodynamic pressures on the laryngeal surface. Since the pressure is greater in the central region of the vocal folds, such region is put in movement before the tissues located in the commissures, causing a difference in the horizontal phase of movements in the vocal fold tissues. The commissure is completely adducted only if the kinetic energy of the tissue is sufficiently large to beat the aerodynamic and elastic forces. The idea of suction is invalid, since the magnitude is very small when compared to elastic resistance of laryngeal tissues. Another possibility for the total glottic adduction is to have reduced initial glottal area (that is, approximation of vocal folds by the laryngeal intrinsic muscles). Thus, the laryngeal movement amplitude can block the air passage through the larynx.
To demonstrate the differences in vertical phase between the movements of various portions of the larynx (including the laryngeal section), a sequential series of images (Figures 4 and 5) is presented. We can notice that the analyzed cycle contains a time interval in which the vocal folds collide and another one in which the glottis remains opened. The tissues located in the upper portion of the vocal folds start the closing movement since the negative pressure (suction) is produced under its surface. The lower portion of the vocal folds suffers the direct action of the pulmonary pressure. During the collision interval, more tissue portions touch each other during the glottic closing interval. When the inertia force (caused by the laryngeal movement) is inferior to the aerodynamic resistance, both vocal folds are set apart.
It is interesting to notice that whereas the inferior portion of the vocal folds is moved from bottom up (in addition to the horizontal movement), the upper portion is brought top down, creating a compression of tissues during the interval of glottal closure.
During the interval in which the vocal folds are apart one from the other, the upper region fibers are pushed upwards. Simultaneously, the middle and lower portions of both vocal folds are slightly close because of the incompressible characteristic of the muscle tissues. These movements are in different phases, that is, all portions of the vocal folds do not close and open simultaneously, but rather in different times. Such difference in phase characterizes the formation of a material wave from bottom up of the vocal folds, normally observed in laryngoscopy exams.
Two larynxes with cancer were simulated to demonstrate the capabilities of the three-dimensional model. In this conception, the vocal folds were maintained wide apart to represent a large sized tumor. In addition, reduced elasticity of laryngeal tissues was included to have compatible extension of the pathology. In order to check if the reduced vibration of the vocal folds is associated with viscoelastic properties of tissues, a second larynx (with cancer) was simulated, in which tissue elasticity was maintained close to that found in normal larynxes.
Figure 6 shows that in both situations the glottal signal is elevated because of the large glottal opening. However, the vibration amplitude decreased with time, up to the stabilization to a relatively constant value. This small oscillation is in large part associated with distribution of pressure along the larynx. Differently from a normal larynx, in which pressure inside the glottis is abrupt, the distribution of pressures in the larynx is more subtle here. Thus, laryngeal tissues (especially the cover) are not sufficiently pressed to establish a sustained exchange of energy between both the physical systems (air and larynx).
When the simulation of unilateral paralysis was conducted, we noticed that primarily the distribution of pressures on the surface of each vocal fold was different. The decrease in pressure on the surface of the normal vocal fold is more abrupt than in the paralyzed fold. It makes the tissues of the normal vocal fold to form material waves with similar characteristics to the waves formed in normal larynxes.
Figure 7 shows that amplitude of glottal signal reaches the oscillatory standard constant after 50ms, since the vocal folds vibrate even under improper aerodynamic conditions. The collision does not occur owing to the large glottal opening.
Finally, two larynxes with vocal sulcus (unilateral) were simulated. The location of the sulci (shown in darker color) is shown in Figure 8. The sulcus is mechanically different from the other laryngeal tissues by its rigid and more viscous consistency. Thus, mathematically, its viscoelastic characteristics are histologically different from the other tissues. Note that additionally the sulcus affects only the cover (epithelium and superficial layer of lamina propria) and it causes modifications of the material wave on the surface of the vocal folds.
The two simulated larynxes (A and B) for vocal sulcus differ only in the location of the sulcus per se. Its effects on vocal fold vibration are significant as shown by Figure 9. Whereas in larynx A there is no vocal fold coaptation, in larynx B, in which the vocal sulcus is located on the vocal fold border, these two structures get together. Additionally, the opening ratio varies, as well as instantaneous fundamental frequency. Such phenomena occur since each vocal fold can have different material waves.
The impossibility of having the approximation of the vocal folds in larynx A is caused by the location of the sulcus. Its mechanical characteristics prevent propagation (from bottom up) of the material wave. Since the sulcus affects specifically the upper portion of one of the vocal folds, in which amplitude of fiber movement is more intense, the adduction of glottis is more restricted. Conversely, the collision of vocal folds in larynx B is facilitated (despite its non-periodicity) since the fibers located on the upper portion of both vocal folds are intact.
Such characteristic is interesting because it shows various aspects of the larynx (anatomical and physiological) that directly influence the formation of the material wave on the vocal fold surface. Thus, the examples of pathological cases simulated in the three-dimensional laryngeal model demonstrated its feasibility for the study of this structure during phonation. Many viscoelastic characteristics in larynxes with some degree of dysphonia were defined based on theoretical conceptions. Experimental assessments of these characteristics are still to be conducted for simulations to become in fact realistic.
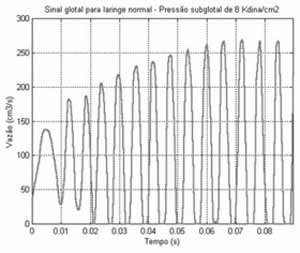
Figura 2. Sinal glotal obtido em simulação de laringe glotal.
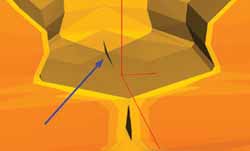
Fig. 3

Fig. 4

Fig. 5
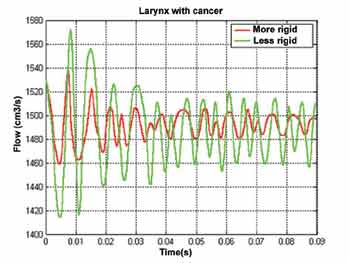
Fig. 6
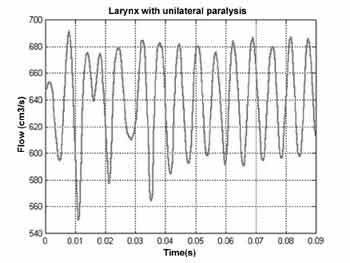
Fig. 7
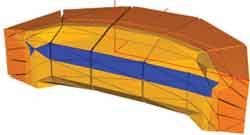
Fig. 8
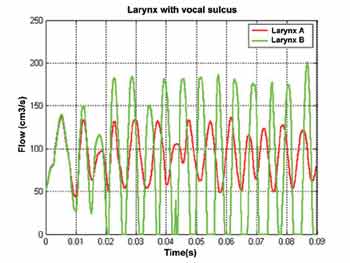
Fig. 9
This study proposed a three-dimensional continuous model of the larynx, considering its anatomical (geometry) and physiological (organic tissue viscoelastic properties) characteristics. Various aspects were studied, such as glottal signal and the influence of various parameters in laryngeal mobility. Such assessments enabled the validation of the model since it is capable of reproducing aspects such as phase differences (horizontal and vertical) in vocal fold movement. The uneven distribution of the aerodynamic pressure (producing a negative pressure over some glottal surface regions) is compatible with the theoretical and experimental studies.
This tool is capable of physiologically simulating the dynamics of the larynx during phonation and can offer great research possibilities for the area. Differently from conventional models, in which the larynx is modeled based on simple structures, the infinitesimal nature of the three-dimensional model enables detailed incorporation of various characteristics of the normal larynx, as well as those affected by some kind of dysphonia. For example, polyps and cysts can be added directly to the virtual surface of the larynx. In addition, larynxes with some type of asymmetry (such as in the case of unilateral vocal fold paralysis) can be simulated, differently from other existing models, such as the two-mass model by Ishizaka and Flanagan (1972).
Pressure measures, movement, material wave speed and flow can be directly included in the three-dimensional model. It enables better understanding of larynx in pathological conditions and appropriate planning of surgical interventions. In the future, such surgeries will be primarily analyzed in the computer so that its feasibility can be assessed.
The presented three-dimensional model enables comprehensive knowledge by otorhinolaryngologists about laryngeal dynamics. A great number of experimental studies still have to be conducted to increase precision of the model, particularly the study of laryngeal tissue viscoelastic properties. However, a first step has certainly been taken, showing a future in which the specialist is going to first virtually assess and operate on the patients' larynx.
REFERENCES1. Alipour-Haghighi F, Titze IR. Elastic models of vocal fold tissues. J Acoust Soc Am 1991;90:1326-1331.
2. Bathe K-J. Finite element procedures. Upper Saddle River. Prentice-Hall Inc.; 1996.
3. Chan RW, Titze IR. Viscoelastic shear properties of human vocal fold mucosa: Measurement methodology and empirical results. J Acoust Soc Am 1999;106:2008-2021.
4. Hertegard S, Gauffin J. Glottal area and vibratory patterns studied with simultaneous stroboscopy, flow glottography and electroglottography. J Speech Hear Res 1995;38:85-100.
5. Hirano M. Phonosurgery: Basic and clinical investigations. Otologia (Fukuoka) 1975;21:239-240.
6. Ishizaka K, Flanagan J. Synthesis of voiced sounds from a two-mass model of the vocal cords. Bell Sys Tech Journ 1972;51:1233-1268.
7. Orlikoff R. Assessment of the dynamics of vocal fold contact from the electroglottogram: data from normal male subjects. J Speech Hear Res 1991;34:1066-1072.
8. Story B, Titze I, Hoffman E. Vocal tract area functions from magnetic resonance imaging. 1996;100:537-554.
9. Story B, Titze I, Hoffman E. Vocal tract area functions for an adult female speaker based on volumetric imaging. J Acoust Soc Am 1998;104:471-487.
10. Titze IR, Talkin D. A theoretical study of the effects of various laryngeal configurations on the acoustics of phonation. J Acoust Soc Am 1979;66:60-74.
11. Titze I, Story B, Burnett C, Holzrichter J, Ng L, Lea W. Comparison between electroglottography and electromagnetic glottography. J Acoust Soc Am 2000;107:581-588.
12. Tran QT, Gerratt BR, Berke GS, Kreiman JK. Measurement of Young's modulus in the in-vivo human vocal folds. Ann Oto Rhino Laryng 1993;102:584-591.


