Departamento de Engenharia Elétrica - Escola de Engenharia de São Carlos - Universidade de São Paulo
Endereço para correspondência: Prof. Tit. José Carlos Pereira - Departamento de Engenharia Elétrica
Escola de Engenharia de São Carlos, Universidade de São Paulo
Av. Trabalhador Sancarlense, 400, Centro 13566-590 São Carlos, São Paulo
Tel (0xx16) 273.9330 - Fax (0x16) 273.9372 - E-mail: pereira@sel.eesc.sc.usp.br
Trabalho financiado pela FAPESP.
INTRODUÇÃOAo longo dos anos, a otorrinolaringologia tem empregado novas técnicas para avaliar as condições da laringe. Desde o uso do espelho de Gancia, para refletir a imagem da laringe, os avanços tecnológicos foram rapidamente incorporados à rotina clínica do especialista, atingindo o estágio sofisticado do registro em vídeo da fonação usando video-laringoscópios, estroboscópios e análises em tempo-real do padrão vibratório das pregas vocais dos pacientes usando computadores.
Imagens de ressonância magnética (Story et al., 1996; Story et al. 1998) permitem que as estruturas da laringe sejam avaliadas quanto ao arranjo anatômico e à constituição orgânica. Entretanto, tal técnica somente permite análises estáticas pois os equipamentos não possibilitam que seqüências de imagens sejam capturadas durante a fonação no intervalo de amostragem exigido para realizar análises em tempo-real.
Fixando-se acelerômetros na região da laringe do paciente (Hertegard e Gauffin, 1995; Orlikoff, 1995) pode-se capturar a vibração das pregas vocais durante o processo fonatório. O sinal glotal (oriundo dessa vibração) assim é determinado e suas propriedades temporais e espectrais são avaliadas e finalmente associadas com as características anatômicas e fisiológicas da laringe. Considerando que o sinal vibratório das pregas vocais é atenuado pelas paredes do pescoço (filtrando as componentes de alta freqüência do sinal glotal), dispositivos magnéticos (Titze et al., 2000) foram projetados de forma a obter um sinal glotal mais imune a tal atenuação.
Atualmente, a análise acústica da voz (Rosa et al., 2000) tem permitido que otorrinolaringologistas avaliem a laringe analisando o padrão do sinal de voz emitido pelo paciente. Através de um conjunto de técnicas matemáticas para quantificação do jitter (perturbação da freqüência fundamental do sinal de voz), do shimmer (perturbação da amplitude fundamental) e da quantidade de ruído, o especialista determina quantitativamente a qualidade da vocalização do paciente e indiretamente as características fisiológicas da laringe.
Combinação destas técnicas permite que o especialista tenha avaliações qualitativas e quantitativas mais precisas da condição patológica da laringe do paciente.
Uma maneira alternativa de avaliar objetivamente a laringe é representá-la através de um modelo biomecânico onde seus elementos estão diretamente relacionados com as propriedades viscoelásticas e geométricas dos tecidos musculares da laringe e físicos do ar. Tal abordagem permite que tanto o sinal glotal quanto o de voz sejam sintetizados e comparados com os sinais equivalentes do paciente. Dessa forma, a modelagem da laringe do paciente permite estudos mais objetivos quanto à dinâmica do processo fonatório.
A literatura tem apresentado modelos simplificados da laringe empregando elementos como massas presas à paredes rígidas por meio de molas e amortecedores. O principal desses modelos é o modelo de duas-massas de Ishizaka e Flanagan (1972), sobre o qual diversos aprimoramentos foram feitos.
As simplificações impostas, tais como simetria da laringe, estruturas matemáticas simplificadas para cálculo do escoamento aerodinâmico e limitado número de estruturas para representação biomecânica das pregas vocais não permitem uma precisa avaliação de como uma doença afeta a laringe e sua vibração. Se forem tomadas doenças como nódulos e pólipos que afetam porções específicas das pregas vocais, tais modelos devem evoluir pela incorporação de mais características anatônicas e fisiológicas da laringe.
Com esse intuito, propomos um modelo tridimensional completo da laringe. Isso envolve definir as propriedades viscoelásticas dos tecidos musculares dessa estrutura, o arranjo de suas fibras, e a geometria tridimensional da laringe. Além disto, desenvolver métodos matemáticos para determinar o comportamento dinâmico do escoamento de ar e dos tecidos musculares.
Uma vez definido, tal modelo tridimensional permite que a laringe do paciente seja avaliada virtualmente. Avaliar os movimentos dos tecidos a partir da cavidade subglotal (algo impossível para a laringoscopia convencional) durante a fonação, a distribuição de pressões sobre as paredes das pregas vocais, a vazão de ar na cavidade glotal, as forças envolvidas na colisão entre as pregas vocais são exemplos de análises que podem ser feitas.
Através de um processo denominado análise-por-síntese, o especialista pode sintetizar os sinais glotal e de voz para compará-los com aqueles produzidos pelo paciente. Isso permite a validação do diagnóstico do especialista pois o modelo estará precisamente reproduzindo as características fisiológicas da laringe do paciente. Avaliações como qual o padrão vibratório dos tecidos na vizinhança de um cisto e qual a quantidade exata de ar escapando pelas fendas fusiformes tornam-se possíveis.
Subseqüente ao diagnóstico, o especialista pode operar "virtualmente" o paciente, verificando a efetividade de uma intervenção cirúrgica antes de sua realização. Um exemplo é a injeção de teflon (ou outro material) em casos de paralisia das pregas vocais para propiciar o fechamento glotal. Conhecidas as características viscoelásticas deste material, o especialista pode avaliar através do modelo tridimensional qual o efeito desta intervenção cirúrgica sobre a vibração das pregas vocais, avaliando qual a posição mais adequada do enxerto, a quantidade necessária de material para propiciar a melhora na condição fonatória do paciente.
O objetivo deste trabalho é apresentar esta nova ferramenta e demonstrar que ela permite que o otorrinolaringologista realize uma avaliação mais objetiva da laringe de seus pacientes usando informações que outrora eram impossíveis de se obter. Além disto, o tratamento "virtual" do paciente é uma tecnologia que permite acelerar a recuperação do paciente após uma cirurgia pois permite que o especialista "teste" suas idéias antes de efetivá-las.
É importante salientar que apesar do forte apelo futurista da abordagem, ela é factível e eleva a atividade clínica do especialista a um novo patamar onde conhecimentos mais elaborados da estrutura orgânica da laringe (suas propriedades viscoelásticas, por exemplo) são exigidos.
Descrição do modelo tridimensional
A primeira etapa na descrição do modelo tridimensional da laringe é sua definição geométrica. Isto é feito dividindo-se a laringe em seções hiperelípticas (pode-se inclusive empregar a técnica de secção milimétricas para determinar a geometria da laringe). Este conjunto de entidades geométricas permite a reconstrução computadorizada da laringe. Adicionalmente pode-se empregar técnicas de modelagem de sólidos para refinar a superfície da laringe digitalizada. A Figura 1 mostra um segmento da laringe digitalizada.
A partir da definição das superfícies que definem a região laríngea a ser analisada, um algoritmo de computador divide o espaço envolvido por tais superfícies em diversos tetraedros. Este conjunto de elementos geométricos é denominado malha. Note que existem duas malhas distintas: uma descreve as estruturas orgânicas da laringe (tecidos musculares e cartilagens) enquanto outra define o espaço por onde o ar escoa. Isto ocorre porque será necessário determinar as velocidades e pressões do ar ao longo da laringe, e isto implica na necessidade de discretização de tal espaço geométrico.
As equações de dinâmica dos sólidos são usadas para descrever matematicamente os deslocamentos da malha da laringe enquanto as equações de Navier-Stokes são usadas no cálculo das velocidades e pressões na malha do escoamento. Estas equações (do tipo diferenciais parciais) descrevem os fenômenos físicos que ocorrem na laringe durante a fonação.
Para representar o escoamento, as equações de Navier-Stokes (Equação 1) são diretamente resolvidas dentro da cavidade laríngea, diferente de Ishizaka e Flanagan (1972) que adotaram uma simplificação destas para determinar a queda de pressão transglotal e a vazão do ar na laringe.
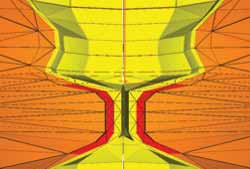
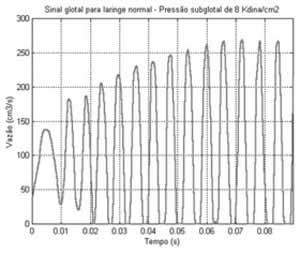
Figura 2. Sinal glotal obtido em simulação de laringe glotal.
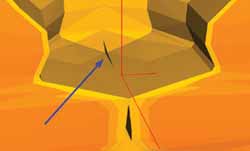
Fig. 3

Fig. 4

Fig. 5
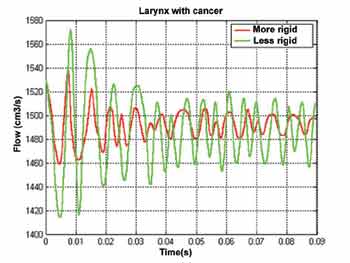
Fig. 6
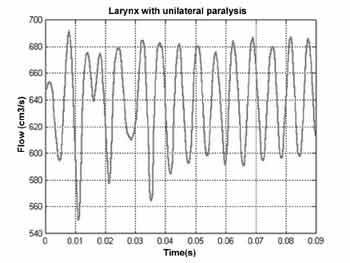
Fig. 7
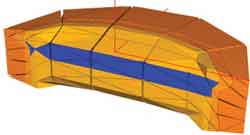
Fig. 8
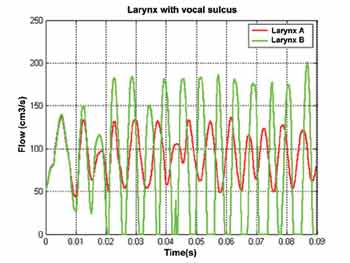
Fig. 9
Onde Uf é o vetor de velocidades, P é a pressão aerodinâmica, rf e mf são a densidade e viscosidade do ar, respectivamente (adotou-se rf =0,000123 g/cm3 e mf =0,000179 dina.s/cm2).
A excitação do escoamento de ar se dá por diferença de pressões. A pressão do pulmão durante a fonação está ao redor de 8 cmH20 enquanto a pressão na epiglote é próxima a pressão atmosférica (zero cmH20) para vogais abertas. Adicionalmente considerou-se que nas paredes da laringe, a velocidade do ar é nula. Tais características - condições de contorno - permitem que as velocidades e pressões ao longo da malha do escoamento sejam calculadas.
Enquanto o escoamento de ar é facilmente descrito pelas equações já citadas, os tecidos da laringe exigem um tratamento especial. Considerando que a orientação das suas fibras se dá ao longo das pregas vocais (longitudinal), um modelo linear transversalmente isotrópico é empregado. Isso ocorre porque as fibras da laringe são mais rígidas na direção longitudinal (ântero-posterior) do que no plano transversal das pregas vocais. Para facilitar a representação matemática, um modelo linear é adotado.
Adicionalmente a diferenciação dos tecidos dentro das pregas vocais é considerado. Seguindo a classificação histológica de Hirano (1975), as pregas vocais apresentam três tipos de tecidos: a cobertura (envolvendo o tecido epitelial e a camada superficial da lamina propria), o ligamento (camadas intermediária e profunda da lamina propria) e corpo (músculo vocal). No modelo, cada um destes tecidos é caracterizado por diferentes propriedades elásticas e de viscosidade. A determinação das propriedades elásticas dos tecidos é feita através de ensaios de distensão do tecido (Chan e Titze, 1999; Alipour-Haghighi e Titze, 1991, Tran et al., 1993) enquanto a viscosidade é definida a partir de características dos tecidos humanos (Titze e Talkin, 1979). Note que a caracterização viscoelástica foi feita a partir de ensaios mecânicos em laringes de cadáveres ou in-vivo (particularmente o módulo transversal de Young E' segundo técnica descrita em Tran et al. (1993)).
Considerando essas características histológicas da laringe, a Tabela 1 apresenta as constantes elásticas que definem os três tipos de tecido no modelo linear transversalmente isotrópico. Note que o módulo de Young transversal E possui amplitude proporcional à profundidade do tecido, conforme comentado em Titze e Talkin (1979). Segundo eles, a rigidez do corpo, ligamento e cobertura deve ser proporcional aos fatores 10:4:2. Esses mesmos autores comentam que a constante de cisalhamento longitudinal m' deve ser mais elevada para o ligamento de forma a representar o seu papel de conexão entre a cobertura e o corpo. Berry e Titze (1996) realizaram um estudo avaliando a influência do par E/m' na vibração das pregas vocais, considerando-as como um sólido compacto. O módulo de Young longitudinal E' é o de mais fácil obtenção. Um valor padronizado foi definido para toda a laringe admitindo-se que tal estrutura tem um comportamento similar quando tracionada, conforme as análises de Alipour-Haghighi e Titze (1991).
A viscosidade é o elemento mais difícil de ser avaliado. Seguindo Titze e Talkin (1979), foi adotado 150 Poise para o tecido do corpo por causa de sua semelhança com outros tecidos humanos de onde este valor foi estimado. Entretanto, para a cobertura e ligamento, esse valor era muito elevado para sustentar a oscilação. Isso ocorria porque tal magnitude viscosa amortecia os movimentos das fibras. Berry e Titze (1996) também empregaram valores baixos para esta constante em suas simulações, mostrando a necessidade de baixa viscosidade para a cobertura, particularmente, de modo que a vibração seja sustentada.
Finalmente, as constantes de Poisson (n e n') foram definidas de forma a manter a quasi-incompressibilidade do tecido muscular. Titze e Talkin (1979) enfatizam que tal característica deve ser mantida para garantir que a vibração dos modelos matemáticos seja compatível com a vibração da laringe real. Como um modelo tensão-deformação linear foi empregado, matematicamente estas constantes devem validar o limite termodinâmico da estrutura, ou seja,(2)
A Equação 2 apenas informa que o sistema muscular descrito não deve produzir energia: apenas mantê-la (sinal de igualdade) ou dissipá-la (sinal de menor).
Como condição de contorno para a resolução das equações da laringe, fixou-se a laringe pela sua superfície externa - deslocamento nulo dos nós que compõe tal superfície. A superfície dita interna - em contato com o escoamento - é excitada pela pressão aerodinâmica, que varia no tempo de acordo com os movimentos das malhas.
O método de elementos finitos (Bathe, 1996) é usado para resolver as equações da laringe e do escoamento por sua facilidade em trabalhar com malhas não-estruturadas (onde os tetraedros diferem geometricamente uns dos outros). Isto é importante porque a laringe movimenta-se e desta forma exige um remapeamento automático de suas novas características geométricas a cada instante de tempo analisado. É importante salientar que não existe solução analítica (exata) para as equações citadas. Assim, o método usado discretiza tais equações para resolvê-las numericamente. Quanto maior é a quantidade de tetraedros (tornando-se assim, menores), mais pontos (ou nós) são empregados para se determinar os deslocamentos espaciais da laringe e as velocidades e pressões do escoamento, e maior é a precisão da solução. Dessa forma, a solução de tais equações paulatinamente aproxima-se da solução exata. Entretanto, a exigência computacional para calcular a quantidade de variáveis existentes torna-se exponencial. Assim, uma boa simulação exige compromissos com precisão e carga computacional.
Adicionalmente, as pregas vocais colidem-se durante a fonação, restringindo a passagem de ar pela glote. Para representar este fenômeno físico, as equações de colisão (ou contato) são derivadas seguindo técnicas comumente encontradas em modelos mecânicos (Bathe, 1996). A idéia central é que deve haver uma força suficiente para evitar a penetração de corpos uns nos outros. Considerando o problema da simulação da laringe, quando as duas pregas vocais se coaptam, forças de ação e reação são produzidas sobre as suas paredes de forma a restringir o seu movimento.
O algoritmo básico que descreve o processo de simulação da laringe é:
1. coleta das pressões aerodinâmicas sobre as paredes da laringe;
2. cálculo dos deslocamentos da laringe quando esta sofre a ação das pressões aerodinâmicas (considerando possíveis colisões);
3. atualização da malha da laringe;
4. atualização da malha do escoamento;
5. cálculo das velocidades e pressões aerodinâmicas do escoamento.
Note que o processo é iterativo. Isto significa que a cada instante de tempo, todas as equações são calculadas seqüencialmente. O acoplamento entre ambos os sistemas físicos (laringe e escoamento de ar) se dá a partir da atualização da malha (nova malha, novo padrão de escoamento de ar) e das pressões aerodinâmicas (compressão da laringe). Os intervalos de tempo entre os ciclos iterativos devem ser bem definidos de acordo com as restrições matemáticas existentes nas equações da laringe e do escoamento e com o grau de detalhamento temporal que se deseja capturar. Os ensaios realizados exigiram intervalos de tempo iguais a 0,0003 segundos.
A simulação é de grande escala pois um conjunto de 15.000 equações para o escoamento e 15.000 equações para a laringe são resolvidas a cada iteração. Isso significa que os deslocamentos de 5.000 pontos da malha são mapeados e calculados em cada instante de tempo. Para o escoamento, a velocidade e a pressão são calculadas em 5.000 pontos dentro da cavidade laríngea. Assim, cada segmento (alguns deles menores que 1 milímetro) da laringe tem sua anatomia e fisiologia representadas no modelo e simuladas.
RESULTADOSPara demonstrar o funcionamento do modelo proposto, uma laringe normal foi simulada. A geometria foi obtida a partir de medições in vivo e de ressonância magnética. Para caracterizar os tecidos musculares, foram utilizadas medidas de viscoelasticidade das fibras obtidas a partir da literatura. Para excitar o modelo tridimensional, as pressões do ar nos pulmões (8 kdina/cm2) e na epiglote (zero dina/cm2) foram definidas, criando a condição aerodinâmica para sustentar o escoamento através da laringe. A Figura 2 mostra o sinal glotal, que corresponde à vazão medida na saída da glote.
Primeiramente percebe-se que as oscilações iniciais são irregulares, caracterizando um transiente. Nesses instantes iniciais, os tecidos da cobertura iniciam sua movimentação, sem entretanto permitirem a colisão entre as pregas vocais.
As colisões entre as pregas vocais somente se iniciam a partir de 20 ms, apesar do intervalo de tempo em que elas permanecem juntas ser bem pequeno. Isso ocorre porque ambas as pregas estão adquirindo energia cinética, vencendo a resistência das forças aerodinâmicas e viscoelásticas (essa última pertencente ao tecido da laringe). É interessante lembrar que quando a viscosidade do tecido (particularmente da cobertura) é excessiva, a energia cinética é insuficiente para vencer a resistência do tecido ao movimento.
A partir de 60 ms a laringe movimenta-se periodicamente, deixando o estado transitório de vibração. Note que a partir deste instante, o sinal glotal alcança sua amplitude máxima. Numericamente o sinal glotal obtido possui 164 Hz com um quociente de abertura igual a 0,6347 (ou seja, em 63,47% do tempo do ciclo completo, a glote fica abduzida e no restante do ciclo ela fica aduzida).
Um interessante fenômeno é observado nas simulações: o fechamento incompleto da glote. Existem situações em que as condições viscoelásticas dos tecidos e a anatomia da laringe impedem a completa adução da glote. Isso provoca um escape de ar cuja vazão é extremamente reduzida. Em situações patológicas, o aparecimento de uma fenda fusiforme na comissura anterior provoca um escape de ar excessivo que afeta a voz do paciente.
Esse fechamento incompleto da glote (conforme mostrado na Figura 3) é causado pela distribuição não-uniforme das pressões aerodinâmicas na superfície da laringe. Como a pressão é maior na região central das pregas vocais, tal região é posta em movimento antes que os tecidos localizados nas comissuras, causando uma diferença de fase horizontal nos deslocamentos dos tecidos das pregas vocais. A comissura somente aduz-se completamente se a energia cinética do seu tecido for suficientemente grande para vencer as forças aerodinâmicas e elásticas. A idéia de "sucção" é invalida pois sua magnitude é muito pequena quando comparada à resistência elástica dos tecidos da laringe. Outra possibilidade para a glote aduzir-se totalmente é a área glotal inicial (ou seja, aproximação das duas pregas vocais por parte dos músculos intrínsecos da laringe) ser reduzida. Assim as amplitudes dos deslocamentos da laringe conseguem bloquear a passagem de ar na laringe.
Para demonstrar a diferença de fase vertical entre os movimentos de diversas porções da laringe (inclusive com um corte da laringe), uma série seqüencial de imagens (Figuras 4 e 5) são apresentadas. Pode-se perceber que o ciclo analisado contém um intervalo de tempo onde as pregas vocais colidem e outro em que a glote permanece aberta. Os tecidos localizados na porção superior das pregas vocais iniciam o movimento de fechamento pois uma pressão negativa (sucção) é produzida sob suas superfícies. A porção inferior das pregas vocais sofre ação direta da pressão pulmonar. Durante o intervalo de colisão, mais porções de tecido tocam-se durante o intervalo de fechamento da glote. Quando a força inercial (causada pelo movimento da laringe) é inferior à resistência aerodinâmica, ambas as pregas vocais são afastadas uma da outra.
É interessante perceber que enquanto a porção inferior das pregas vocais é movimentada no sentido de baixo para cima (além do seu movimento horizontal), a porção superior é trazida para baixo, criando uma compressão de tecidos durante o intervalo de fechamento glotal.
Durante o intervalo em que as pregas vocais são afastadas uma da outra, as fibras da região superior são "empurradas" para cima. Simultaneamente, as porções média e inferior de ambas as pregas vocais são ligeiramente aproximadas por causa da incompressibilidade dos tecidos musculares. Estes movimentos estão em fases diferentes, ou seja, todas as porções das pregas vocais não se fecham ou abrem simultaneamente mas sim em instantes de tempo diferentes. Tal diferença de fase caracteriza a formação da onda material de baixo para cima das pregas vocais, normalmente observado em exames de laringoscopia.
Duas laringes com câncer foram simuladas para demonstrar as capacidades do modelo tridimensional. Nesta concepção, as pregas vocais foram mantidas bem afastadas para representar um câncer de grande extensão. Adicionalmente a elasticidade dos tecidos da laringe foi reduzida de forma a compatibilizar a extensão da patologia. Para verificar se a pouca vibração das pregas vocais está ou não associada às propriedades viscoelásticas dos tecidos, uma segunda laringe (com câncer) foi simulada, na qual a elasticidade dos tecidos é mantida próxima daquela encontrada em uma laringe normal.
Na Figura 6, pode-se notar que em ambas as situações, o sinal glotal é elevado por causa da grande abertura glotal. Entretanto, as amplitudes das vibrações decaem ao longo do tempo, até se estabilizarem em um valor aproximadamente constante. Essa pequena oscilação está associada em grande parte à distribuição de pressões ao longo da laringe. Diferente de uma laringe normal, na qual a queda de pressão dentro da glote é mais abrupta, a distribuição das pressões ao longo da laringe é mais suave. Assim, os tecidos da laringe (principalmente a cobertura) não são pressionados suficientemente para estabelecer uma troca sustentada de energia entre ambos os sistemas físicos (ar e laringe).
Quando a simulação de uma paralisia unilateral foi conduzida, percebeu-se primeiramente que a distribuição de pressões na superfície de cada uma das pregas vocais era diferente. A queda de pressão na superfície da prega vocal normal é mais abrupta do que na prega paralisada. Isso faz com que os tecidos da prega vocal normal formem ondas materiais com características similares às ondas formadas em laringes normais.
A Figura 7 mostra que as amplitudes do sinal glotal atingem um padrão oscilatório constante a partir de 50 ms, uma vez que uma das pregas vocais vibra mesmo sob condições aerodinâmicas impróprias. A colisão não ocorre devido à grande abertura glotal.
Finalmente, duas laringes com sulcos vocais (unilateral) foram simuladas. A localização desses sulcos (em tonalidade mais escura) é mostrada na Figura 8. O sulco diferencia-se mecanicamente dos demais tecidos da laringe pela sua consistência mais rígida e mais viscosa. Assim, matematicamente, suas características viscoelásticas são histologicamente diferentes dos demais tecidos. Note adicionalmente que o sulco afeta somente a cobertura (epitélio e camada superficial da lamina propria) e isto provoca modificações na onda material na superfície das pregas vocais.
As duas laringes simuladas (A e B) para o sulco vocal diferenciam-se apenas na localização do sulco propriamente dito. Seus efeitos na vibração das pregas vocais são significativos como mostra a Figura 9. Enquanto na laringe A, a coaptação entre as pregas vocais não ocorre, na laringe B, na qual o sulco vocal localiza-se na borda da prega vocal, essas duas estruturas se encontram. Adicionalmente o quociente de abertura varia, juntamente com a freqüência fundamental instantânea. Tais fenômenos ocorrem pois cada uma das pregas vocais possuem ondas materiais diferentes.
A impossibilidade de encontro entre as duas pregas vocais na laringe A é devido a localização do sulco. Suas características mecânicas impedem a propagação (de baixo para cima) da onda material. Como esse sulco afeta justamente a porção superior de uma das pregas vocais, onde a amplitude dos movimentos das fibras é mais intenso, a adução da glote fica restrita. Em contrapartida, a colisão das pregas vocais na laringe B é facilitada (apesar de não-periódica) pois as fibras localizadas na porção superior de ambas as pregas vocais estão intactas.
Tal característica é interessante pois mostra que os diversos aspectos da laringe (anatômicos e fisiológicos) influenciam diretamente a formação da onda material na superfície das pregas vocais. Assim, os exemplos de casos patológicos simulados no modelo tridimensional da laringe demonstram sua viabilidade para o estudo do comportamento dessa estrutura durante a fonação. Muitas das características viscoelásticas em laringes com alguma disfonia foram definidos a partir de concepções teóricas. Avaliações experimentais destas características ainda precisam ser conduzidas para que as simulações sejam mais realistas.
CONCLUSÃOEste trabalho propôs um modelo tridimensional e contínuo da laringe, considerando suas características anatômicas (geometria) e fisiológicas (propriedades viscoelásticas dos tecidos orgânicos). Diversos aspectos foram estudados como o sinal glotal e a influência de diversos parâmetros na mobilidade da laringe. Tais avaliações permitiram a validação do modelo pois esse foi capaz de reproduzir aspectos como a diferença de fase (horizontal e vertical) na movimentação das pregas vocais. A distribuição não-uniforme da pressão aerodinâmica (produzindo uma pressão negativa sobre algumas regiões da superfície glotal) são compatíveis com estudos teóricos e experimentais.
Tal ferramenta é capaz de simular fisiologicamente a dinâmica da laringe durante a fonação e estabelece enormes possibilidades de pesquisa na área. Diferente de modelos convencionais, onde a laringe é modelada a partir de estruturas simples, a natureza infinitesimal do modelo tridimensional permite a incorporação detalhada das diversas características de uma laringe normal, assim como daquelas acometidas por alguma disfonia. Por exemplo, pólipos e cistos podem ser adicionados diretamente sobre a superfície "virtual" da laringe. Adicionalmente, laringes com algum tipo de assimetria (como no caso da paralisia unilateral de prega vocal) podem ser simuladas, diferente de outros modelos existentes, como o duas-massas de Ishizaka e Flanagan (1972).
Medições de pressão, deslocamento, velocidade da onda material e vazão podem ser realizadas diretamente no modelo tridimensional. Isso permite que a laringe em condições patológicas seja melhor compreendida e intervenções cirúrgicas sejam planejadas adequadamente. Futuramente, tais cirurgias poderão ser primeiramente realizadas "dentro do computador" e sua viabilidade avaliada.
O modelo tridimensional apresentado permite, assim, um grande aprofundamento do conhecimento de otorrinolaringologistas sobre a dinâmica da laringe. É certo que uma grande quantidade de estudos experimentais necessitam ser conduzidos para elevar o grau de precisão do modelo, particularmente o levantamento das propriedades viscoelásticas dos tecidos da laringe. Mas certamente, um primeiro passo está sendo dado, vislumbrando um futuro onde o especialista avaliará e operará virtualmente a laringe de seu paciente.
REFERÊNCIAS BIBLIOGRÁFICAS1. Alipour-Haghighi F, Titze IR. Elastic models of vocal fold tissues. J Acoust Soc Am 1991;90:1326-1331.
2. Bathe K-J. Finite element procedures. Upper Saddle River. Prentice-Hall Inc.; 1996.
3. Chan RW, Titze IR. Viscoelastic shear properties of human vocal fold mucosa: Measurement methodology and empirical results. J Acoust Soc Am 1999;106:2008-2021.
4. Hertegard S, Gauffin J. Glottal area and vibratory patterns studied with simultaneous stroboscopy, flow glottography and electroglottography. J Speech Hear Res 1995;38:85-100.
5. Hirano M. Phonosurgery: Basic and clinical investigations. Otologia (Fukuoka) 1975;21:239-240.
6. Ishizaka K, Flanagan J. Synthesis of voiced sounds from a two-mass model of the vocal cords. Bell Sys Tech Journ 1972;51:1233-1268.
7. Orlikoff R. Assessment of the dynamics of vocal fold contact from the electroglottogram: data from normal male subjects. J Speech Hear Res 1991;34:1066-1072.
8. Story B, Titze I, Hoffman E. Vocal tract area functions from magnetic resonance imaging. 1996;100:537-554.
9. Story B, Titze I, Hoffman E. Vocal tract area functions for an adult female speacker based on volumetric imaging. J Acoust Soc Am 1998;104:471-487.
10. Titze IR, Talkin D. A theoretical study of the effects of various laryngeal configurations on the acoustics of phonation. J Acoust Soc Am 1979;66:60-74.
11. Titze I, Story B, Burnett C, Holzrichter J, Ng L, Lea W. Comparison between electroglottography and electromagnetic glottography. J Acoust Soc Am 2000;107:581-588.
12. Tran QT, Gerratt BR, Berke GS, Kreiman JK. Measurement of Young's modulus in the in-vivo human vocal folds. Ann Oto Rhino Laryng 1993;102:584-591.


