IntroductionIn order to increase our knowledge about the behavior of the vestibular system in health and disease quantitative methods for assessing vestibular function were developed.
The gradual evolution towards objective measurements of vestibular function began with the clinical observations by Bárány6. Electronic recordings of eye movement to produce permanent records, the hand measurement of nystagmus parameters and the subsequent use of electronic integrators and averagers are developments in this direction.
By the recent application of digital computers to the analysis of eye movement and by the development of precise visual and vestibular test stimuli1, 2, 5 a quantitative relationship between stimulus and response has been estabilished for a normal population. By applying the same methods of measurement to patients with known lesions, quatitative differences from the norm were obtained.4
Eye movement recording and computer sampling
Horizontal eye movement was recorded using electrodes at the outer canthi of the eyes with a reference electrode at the center of the forehead and with the aid of electronic amplifiers developed in our laboratories. The stimuli were visual or vestibular. Visual stimuli consisted of two pypes: 1) a dot of ligh moving across a television screen with a constant velocity at various frequencies or through a randomly presented series of varied amplitude jumps, and 2) no optokinetic drum rotating in both directions at a constant velocity or rotating at an increasing velocity to a maximum of 81°/sec. and then decreasing to zero velocity.
The vestibular stimuli consisted of positional tests, caloric stimuli of 30° and 44° for 40 seconds in each ear, randomly presented series of impulses created by producing sudden changes in table velocity of 16, 32, 64, 128 and 256°/sec. clockwise and counterclockwise, and sinusoidal table movements at 0.05 Hz using peak table velocities of 15, 30, 60, 120°/sec. In one group of subjets the sinuoidal test was carried out at frequencies from .01 Hz to .12 Hz, at a maximum velocity of 30, 60, 90, and 120°/sec.
Polygraph chart recordings of eye movements were used for continuous monitoring of the test as well as to provide records for laser reference. The signal from subject was simultaneously recorded on a four channel FM tape recorder and digitized in the computer. The computer sampled each channel 200 times per second (Fig. 1).
Analysis of nystagmus
The analysis of the nystagmus consists of identifying the time and amplitude of each maximum and minimum in a nystagmus beat. From these "minmax" points, the values of seven parameters associated with each nystagmus beat can be determined. This information can then be displayed either graphically or as a table numbers. As an example the time course of six of these parameters are shown in Fig. 2 for every nystagmus beat occurring during an optokinetic response (drum rotated at 30° cw). Additional examples of nystagmus analysis are shown for the slow component velocity for each nystagmus beat in response to a caloric stimulus (Fig. 3), to a constant angular acceleration of the subject (Fig. 4), to a sudden change in angular velocity (Fig. 5), to a sinusoidal movement (Fig. 6), and to an optokinetic ramp (Fig. 7).
Analysis of eye tracking
Two distinct patterns of eye tracking are tested. These are pursuit and saccadic eye movements. For the pursuit task a dot of light displayed on a large television screen is moved back and forth across the screen at a constant velocity for several cycles. The computer calculates the velocity of the eye 50 times/sec. and then plots a velocity distribution histogram for the entire sample.
For the saccade task a dot of light on a large television screen moves randomly through a series of sudden movements of the same or different amplitude. As the dot is perceived in the peripheral visual field, the eyes are moved in one or more saccades to fix the foviae on the target. The computer is used to calculate the average and maximum velocity of each saccade and to plot it in relationship to the amplitude of that particular saccade. The equation EV - Vmax (1 - Exp (- A/L) is then used to quantify the relationship by plotting a best fit curve to the data. (EV - eiter the average or maximum velocity of the saccade; Vmax = theoretical maximum velocity attained by the curve; A - amplitude of saccade; L - curvature parameter). Fig. 8 illustrates the tracking sequence in a normal sublet.
Statistical programs
In order to obtain clinically useful information from this tremendous quantity of data it was necessary to develop statistical programs. One such program compares the seven parameters of nystagmus with each other and plots the degree of correlation between parameters (Fig. 9).
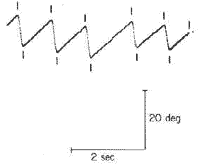
Figure 1. The computer samples each channel 200 times per second. It then flags the points where each slow component each fast component starts.
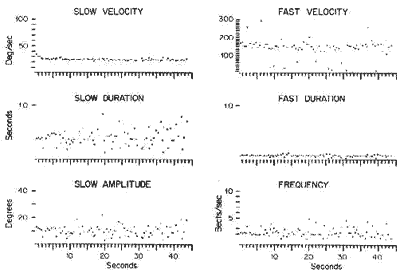
Figure 2. Six parameters of nystagmus for every nystagmus beat in an optokinetic response are graphically plotted.

Figure 3. The slow component velocity of the eye in response to a 40 second caloric stimulation at 33° C.
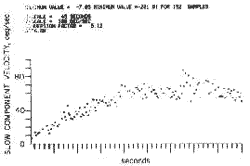
Figure 4. The slow component velocity of the eye in response to a constant acceleration stimulus of 6°/sec.²
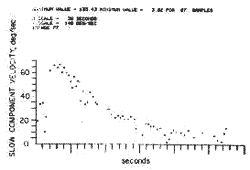
Figure 5. The slow component velocity the eye in response to a sudden 128° sec. change in table velocity.
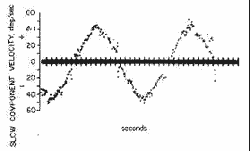
Figure 6. The slow component velocity of the eye in response to a sinusoidal table movement at 0.01 Hz, maximum table velocity 60°/ sec.
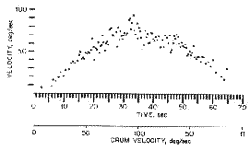
Figure 7. The slow component velocity of the eye response to an optokinetic ramp. Drum velocity 0 ? 80. 80 ? 0°/se.
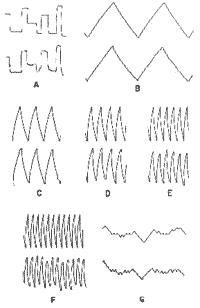
Figure 8. Tracking sequence in a normal subject. a) random sequence of saccades, b) pursuit at 0.1 Hz, c) pursuit at 0.3 Hz, d) pursuit 0.5 Hz, e) pursuit at 0.7 Hz, pursuit at 0.9 Hz, g) random chance in constant velocity (being developed).
There are differences in the correlation coefficients in nystagmus resulting from different stomuli. In order to examine the time course of nystagmus parameters induced by different stomuli, curve fitting programs were developed which plot the best fit curve from the data points obtained from the patient (Figs. 10, 11, 12). From these curves the time constants of the response, or a mathematical desaiption of a relationship between two variables as well as the quality of fit of the data to the theoretical curve can be obtained. From such values quantitative information about the normal systen has been obtained.

Figure 9. Correlation matriz between the nystagmus parameters in d response to a sudder, change in table velocity. Parameters are: SA = slow component amplitude; FA - fast component amplitude; SV= solow component velocity; FV = fast component velocity; SD = slow component duration; FD = fast component duration; Freq = frequenry.
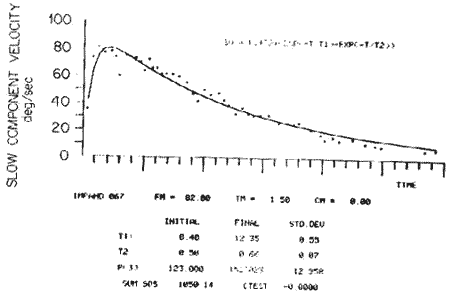
Figure 10. Curve fitting program for response to sudden change in table velocity. T1 the rising time constant and T2 the falling time constant are automatically computed.
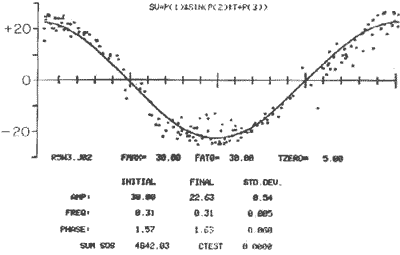
Figure 11. Curve fitting program for response to sinusoidal stimulation. The maximum amplitude, the frequeacy and the phase in respea to the stimulus are automatically computed.
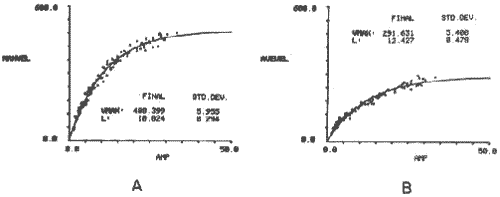
Figure 12. The relatioaship between the amplitude and velocity of the saccade is plotted for each saccade and the best fit curve to the data is automatically computed. A. maximum velocity for each saccade B. average velocity for each saccade.
Results in normal subjects
By using series of precise stimuli an attempt was made to probe the physiologic range of the normal system and to establish information about the relationship between stimulus and response.
Several examples of such stimulus response relationships are shown. The relationship between the velocity change of the turntable (?) and the maximum slow component velocity of the nystagmus response in the impulsive test is shown in Pig. 13. The relationship between the optokinetic drum velocity and slow component velocity of optokinetic nystagmus is shown in Fig 14. For sinusoidal stimulation, the relationship between maximum table velocity and maximum eye velocity at different frequencies can also be established (Fig. 15). The relationship between amplitude and average or maximum velocity in the saccade task (random steps) was determined for a normal population. The distribution of eye velocities in the pursuit task at constant target velocities was also determined for a normal population. An example of a normal response to three different target velocities (.1, .5, and .9 Hz) is shown in Fig. 16.
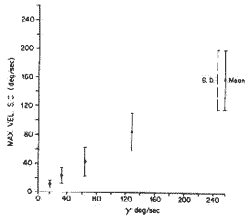
Figure 13. The relationship between sudden change in table velocity (?) versus the maximum slow component velocity of the eye in a normal population.
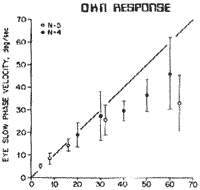
Figure 14. The relationship between optokinetic drum velocity and average slow component velocity of the eye.
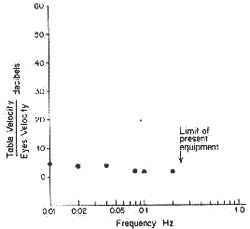
Figure 15. The relationship between maximum table velocity and maximum slow component velocity at various frequencies for sinusoidal stimulation.
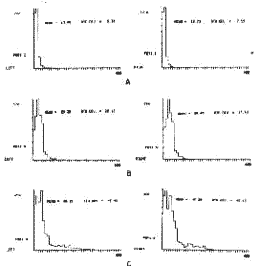
Figure 16. In the pursuit task the computer determines the velocity of the eye 50 times/sec. and plots a velocity distribution histogram and computes mesa velocity and standard deviation. A 0.1 Hz target velocity 6°/sec. B. 0.5 Hz target velocity 30°/ sec. C. 9 Hz target velocity 54°/sec.
Results in patients
Similar methods have been applied to the testing of patients with lesions whose anatomic site is known either on the basis of clear cut otoneurological signus or from radiographic, surgical, or post mortem verification.
A patient with severe bilateral reduced peripheral vestibular function still responded to impulsive stimulation in a measurable way (Fig. 17). A patient with multiple sclerosis did reasonably well in one form of optokinetic task (both eyes open), but exhibiced virtually no relationship between drum velocity and eye velocity when the right eye was closed (Fig. 18). A patient with unilateral peripheral vestibular paralysis responded below the range for the normal population and responded differently in the clockwise and counterclockwise directions during the impulsive test (Fig. 19). A patient with cerebellar degeneration showed a greater response than the normal population in the impulsive test (Fig. 20).
In the pursuit task as well as in the saccade task patients with pure cerebellar disease or patients with cerebellar and brain stem disease showed a clearly different response from the normal population (Figs. 21, 22).
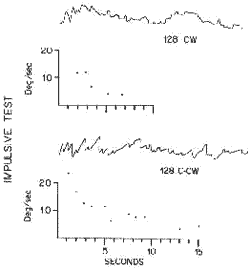
Figure 17. The slow component responses to 128°/sec. CW and CCW sudden change in table velocity in a patient with bilateral Meniere's.
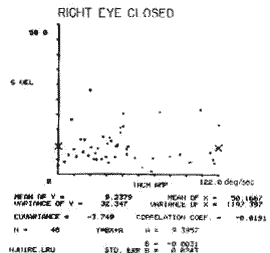
Figure 18. A patient with multiple sderosis has virtually no correlation between optokinetic drum velocity and eye velocity when left eye clowd (Correlation coefffcient - 0.0191).
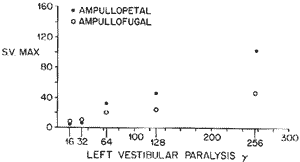
Figure 19. Shows the relationship between (?) change in table velocity and maximum slow component velocity of the eye in a patient with unilateral peripherai vestibular paralysis (compare with fig. 13).
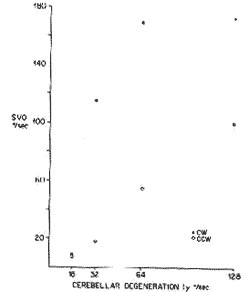
Figure 20. Shows the relationship between (?) change in table velocity and maximum slow component velocity of the eye in a patient with cerebellar degeneration (compare with Fig. 13).
Discussion:
From the first clinical observations of eye movements to the present there has been a gradual evolution toward more objective evaluation for the diagnosis of diseases of the oculovestibular system.
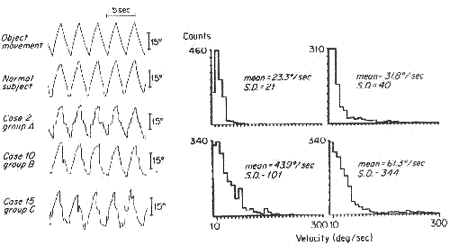
Figure 21. The velocity distribution histogram in the pursait task at 300 sec 0.5 Hz in a normal subject (left upper hhistogram), a patient with cerebellar degenerarion (right upper), a patient with oliva-ponto-cerebellar degeneration (left lower), and a patient with Friedreich's ataxia (right lower)
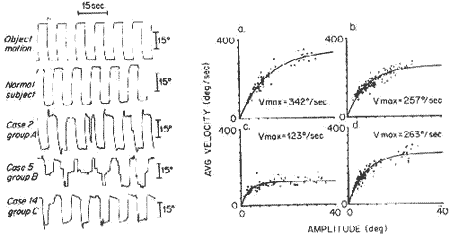
Figure 22. The relatioaship between saccade amplitude and velocitp: a) normal subject. b) a patient with cerebellar degeneration. c) a patient with oliva-ponto cerebellar degeneration. d) a patient with Friedreich's ataxia. All these patieats show slowing of sacades.
The application of digital computers to the analysis of eye movements is a recent attempt to continue this development. Because of the speed and versatility of modern digital computers the analysis of such data is limited only by the imagination of the investigatiors and by their theoretical understanding of the behavior of the system under study. By the cooperation of investigators from many disciplines (mathematics, physics, engineering, physiology, clinical neurology and otolaryngology) the specialized skills developed in these disciplines can be brought to tear on the subject. This ability to handle large amounts of data has in turn made practical the utilization or precise test stimuli in order to probe the physiologic range of these systems.
Statistical programas which average, curve fit, and plot relationships between stimulus and response and between various parameters of response are aimed at producing more meaningful, more comprehensive and more predictive information about the vestibular system. The fact that, in patients with anatomically discrete lesions, quantitatively different responses ocular gives us encouragement that these methods will become diagnostically useful.
In order to determine the best set of tests to use in a diagnostic work up, many patients with known lesions will have to undergo extensive testing. What will probably emerge is a brief series of screening tests, the results of with will then suggest additional tests to clearly delineate the extent of the lesion and quantitatively measure the physiologic loss. Continuing work with normal and pathological populations is necessary to increase our theoretical understading and to perfect the tests so that with a minimal amount of discomfort and testing time, a comprehensive evaluation of the patients vestibulo-visual-occulomotor function can be obtained.
References:1- Honrubia V, Kats R, Strelioff D, Jankins H. and Word P.: Computer analysis of induced vestibular and optokinetic nystagmus. Annals of Otol. Rhinol. Laryngol. 80(6) Suppl. 3, December, 1971.
2- Konrad H and Sill A.: The application of Small computers to the solution of clinical problems. Amer. College of Surgeons. 59th Clinical Congress. Surgeons Forum, October, 1973.
3- Hulk J and Jongkess LBW.: The turning test with small regulable stimuli. II. The normal cupulogram. J. Laryngol. Otol. 62: 70-75, 1948.
4- Balob R, Konrad H.: Honrubia V. Vestibulo-ocular function in patientts with cerebellar atrophy. In preparation.
5- Honrubia V, Streliof f D, and Word P. Computer analysis of nystagmus induced by constant angular acceleration in normal and labytinthectornized cats. Adv. Oco-Rhino-Laryng., 19: 254-265 (Karger, Basel) 1973.
6- Bárány R.: Physiologie und Pathologie des Bogengangaspparates beim Menschen. Du-e ticke, Leipzig and Wien, 1907.
Endereço do Autor
10833 Le Conte Ave. - Los Angeles, Calif. 90024.
From the Head and Neck Surgery Division, UCLA Medical Center, and Department of Neurology,*
UCLA Medical Center. This work was supported by NIH Grant USPHS NS 09823.


