Versão Inglês

Ano:  1942  Vol. 10   Ed. 6  - Novembro - Dezembro - (4º)

Seção: -

Páginas: 635 a 645

GRAFICO AUDIOMETRICO PELOS DIAPASÕES

Autor(es): DR. ANGELO MAZZA
ACADEMICO NICOLAU MAZZA

S. Paulo

O conceito médico - aprimorar os metodos de exame para melhor terapeutica - encontra na semiologia otologica a sua razão de ser.

Entre os varios elementos utilisados para a avaliação da funcção auditiva os diapasões constituem, sem duvida, o de maior significação. As provas acusticas Weber, Rinne, Schwabach etc., de reconhecido valor na localisação de lesão, exprimem a utilização maxima dos diapasões.

O exame de rotina da função auditiva pelos mesmos, primam, antes, pela qualidade, do que, pela quantidade. Em outras palavras eles conferem, de preferencia, o tipo, a natureza da surdez, mais do que, seu grau. Com o progresso da otologia, fisicos e otologistas crearam, para uniformisar os resultados, a unidade de intensidade de som.

Convencionou-se, assim, identificar a decima parte do Bell, (decibel (db), como unidade "standard" para a medida de intensidade do som. Todo o individuo hipoacusico, pondera YATES, necessita maior intensidade na emissão do som, do que uma pessoa normal, para estimular seu ouvido afectado.

Será intuitivo, pois, exprimir os resultados em Decibels e não em segundos de audibilidade.

Este trabalho tem por objecto apresentar um grafico da curva auditiva obtida pelos diapasões e medida em decibels, o qual, é construido por um artificio, fundamentado, de um lado na equação de FLETCHER, que, representa a perda de audição, e por outro, na lei obedecida pelo movimento vibratorio dos diapasões.

Evidentemente este grafico atinge, apenas, onde alcançam as possibilidades clinicas dos diapasões.

Sim, para o exame da condução aerea, estes instrumentos, conferem um resultado audiografico apreciavel, o mesmo não acontece com a condução ossea, onde, ele, são de uso limitado, sobretudo, para as frequencias elevadas (ou altas).

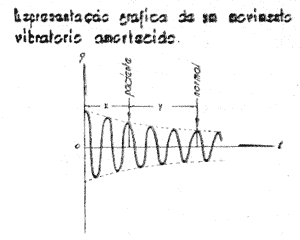
O grafico foi construção com a serie de Hartmann correspondendo respectivamente a c, c1, c2, c3, c4 da escala musical, Cada um deles possue a sua frequencia (N.º de DV por segundo) definida, respectivamente 128, 256, 516, 1024 e 2048 DV. Esta frequencia é sempre constante por cada diapasão, independentemente da intensidade elo sons emitido. Percutido o diapasão o movimento vibratorio sofre um amortecimento uniforme, regular, sempre de certo grau (db por segundo), constante para cada diapasão. Cada um deles possue a sua constante de amortecimento.

E. P. FOWLER determinou as constantes de uma serie de diapasões calibrados:

D.V. Db por seg.
128 - 1,08
256 - 1,38
512 - 1,31
1024 - 1,70
2048 - 2,17

De uma maneira geral, o amortecimento é tanto mais rapido quanto mais elevada for a frequencia.

O que se deve exigir na construção de um grafico da acuidade auditiva?

1.º - Que seja de simples feitora;

2.º - Que seja eficaz e flor conseguinte pratico; isto é, cuja curva audiografica seja medida em unidades de sensação ou decibels. Enfim que seja expresso em linguagens universalmente: adotada.

3.º - Que seja função de propriedades fisicas dos diapasões isto é, cuja escala audiometrica esteja relacionada parra cada frequencia, com as respectivas constantes de amortecimento em segundos de audibilidade.

A idéia de grafar e medir a acuidade auditiva pelos diapasões, é, consequencia logica, da distribuição, em serie progressiva, das frequencias de um lado (abcissa), e de outro, a escala da perda de audição (ordenadas).

Diversos autores cada qual a seu modo, tentaram introduzir respectivamente seus metodos. Destes, citaremos sumariamente, os de ROTH, VATES e JOHNSON, após os quais, apresentaremos o nosso. Seja qual fôr o grafito adotado, o seu maior merito é a sistematisação dos exames de rotina pelos diapasões.

PROCESSO PRIMITIVO DE ROTH

Este autor em 1932 imaginou um processo inteligente, porem, rudimentar.

Ele mede a diferencial acustica entre o paciente e o examinador (normal). Lança-a no grafito previamente construido e cuja ordenada é medida em segundos de audibilidade.
Inferiormente ao grafito vê-se a linha representativa da surdez maxima. Notar que esta linha é quebrada, isto é, um pessimo ponto de referencia.

Dos treis quesitos acima enunciados a simplicidade é a unica vantagem deste metodo. Este foi abandonado pelo autor e substituido por outro mais aperfeiçoado.


METODO DE JOHNSON

O processo de JOHNSON é de todos os mais engenhoso, porem, o menos pratico e pouco eficaz.

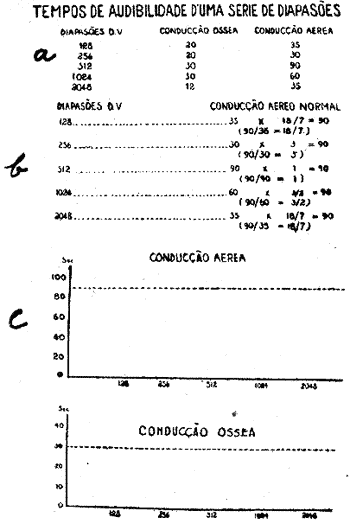
Com percussão uniforme verifica-se o tempo de vibração de todos os diapasões seja em relação á condução aerea quanto á condução ossea. (V. fig. 1-a)

Observa-se que o maior tempo da condução aerea é 90". Multiplica-se o tempo de cada diapasão por uma fracção na qual o numerador seja sempre 90 e o denominador os outros tempos respectivamente. (V. fig. 1-b)

Procede-se do mesmo modo com a condução ossea, na qual o maior tempo é 30". Reduzidos assim á uma base comum todos os tempos, em segundos, de cada diapasão seja para a conducção aerea como para a ossea, os graficos podem ser construidos como segue. (V. Fig. 1-c)

Fig. 1 - Metodo de Johnson

Os tempos obtidos no paciente só serão lançados no grafico depois de serem previamente multiplicados respectivamente pelas frações de base comum.

Estes resultados assim serão definitivos. Após a conducção aerea, repetir "mutatis mutandis" para a conducção ossea.

NOVO GRAFICO DE ROTH

(Diapasões audiometricos)
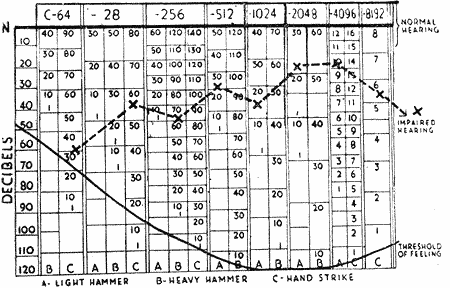
ROTH um dos mais estudiosos do assunto dá á lume em 1.941 um novo metodo. Modifica o modelo classico de diapasão creando novos tipos, munidos de martelos desmontaveis. Conforme o grau de surdez do paciente usa o martelo leve ou pesado. No cabo existe um coletor de som.
DR. ANGELO MAZZA E ACADEMICO NICOLAU MAZZA

Os martelos estão justapostos aos diapasões de tal modo a percutirem as astes sempre com a mesma intensidade. Quanto ao grafico procura imitar a tabela do audiometro.

Como neste a curva audiometrica em decibels obtida está entre os limiares de audibilidade e o de sensação. A coluna total das frequencias mede em segundos de audibilidade. Cada coluna total está subdividida em colunas estreitas correspondendo cada uma aos tempos, conforme, a percussão do martelo é fraca. forte, ou coro a mão.

Fig. 2 - Coletor de som em contáto cem o ouvido. (Diapasão de Roth).

A intensidade inicial (em decibels) é dada por tini indicador de som (audiometro etc.). A relação entre os tempos (segundos) com os decibels é facilmente deduzida, desde que, se conheça a constante de amortecimento, em decibels por segundo, de cada diapasão.

Corno se vê, conforme o autor o classifica é um diapasão audiometrico e seu grafito endossa todos os itens acima referidos, A sua vantagem maxima é que o mesmo pôde ser realizado com a serie completa de diapasões, e, cora as frequencias reais elevadas.
Porem só pode ser realizado com os diapasões do autor. Necessita de percussão inicial sempre uniforme. Alem disso calibra-los com uma fonte sonora de intensidade (em decibels) conhecida.

GRAFICO AUDIOMETRICO PELOS DIAPASÕES

Fig. 3 - Grafico recente de Roth onde se procura imitar a tabela audiometrica.

AUDIOGRAFIA DE YATES

YATES, ilustre otologista de Londres apresenta tambem um metodo grafico de grande alcance por encerrar todos os elementos qualitativos, quantitativos a par das provas acusticas e da voz. Deixa de ser pratico, sobretudo porque é medido em unidade especialmente creada pelo autor, isto é, em "Half-intensity period".

E, finalmente, apresentaremos o nosso metodo

GRAFICO AUDIOMETRICO PELOS DIAPASÕES

FLETCHER, partindo de dados fisicos e fisiopatologicos deduziu uma equação cuja base fundamental está na lei que rege as sensações.

Perda de audição = 10 log. 10 I/Iº

Sendo I a intensidade necessaria para o paciente ouvir e I° a intensidade do som para audição normal. Esta equação, acentua FLETCHER, traduz a perda de audição para qualquer som seja ele puro, musical, voz ou diapasão.

DR. ANGELO MAZZA E ACADEMICO NICOLAU MAZZA

O mesmo autor relacionou-a á seguinte expressão matematica conhecida em dinamica:

log. e I/I° = ß (to - t)

(beta) ß é uma constante de proporcionalidade.
t = tempo de audibilidade do hipoacusico.
t° = tempo de audibilidade da pessoa normal.

Conclue-se pois a perda de audição (expressa em unidades de sensação) é proporcional á diferença de tempos em segundos

P. A. =(to- t)

(delta) é a constante de proporcionalidade, dada pelo amortecimento do diapasão.

Pois bem, o nosso metodo repousa no desenvolvimento gráfico dessa equação.

O nosso diagrama consiste em medir a acuidade auditiva do paciente, em segundos de audibilidade, com os diapasões, por intermedio da formula P. A. = (t° - t)

Este diagrama é constituido de colunas verticalmente dispostas e divididas em segundos.

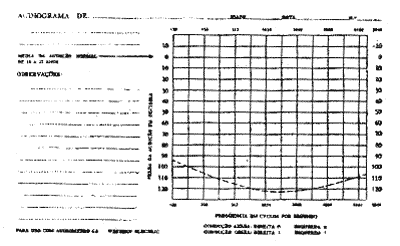
Cada coluna correspondendo a uma determinada frequencia. Estas, são encaixadas no espaço livre, no interior da ficha do audiometro. (Neste estudo entende-se a do Western Electric 6A).

Fig. 4 - Modelo de uma ficha audiometrica do Western Electric 6A por meio da qual é feito o nosso diagrama.

Utilisamo-nos, apenas, do esqueleto da ficha audiometrica, isto é, de seus pontos de reparo
Escala da perda de audição em db. (ordenada) das frequencias (abcissa) limiar de sensação (surdez total) e o limiar de audibilidade (nivel o da ficha de audição normal). Fig. 5.

Fig. 5 - DIAGRAMA PELOS DIAPASÕES Este diagrama é a superposição da ficha audiometrica (W. E. 6A) contendo no seu interior colunas verticais divididas em segundos de audibilidade obtida pela equação de Fletcher.

Em outras palavras, a ordenada, e, a abcissa servem de moldura para as colunas divididas das frequencias (expresso em segundos).

Para adotar essas colunas na ficha, deve-se realizar de tal modo, que a surdez total, pelos diapasões, de cada frequencia coincida respectivamente com a do audiometro (medida em decibel).

Identicamente devemos superpôr o nivel zero (audição normal) de ambos os instrumentos.

CONSTRUCÇÃO DO DIAGRAMA

Em 1.° lugar façamos a superposição do limiar de audibilidade (nivel 0 de audição normal).

Para o 128 d. v.:

Partindo da formula P. A. = (t0 - t).

Quando o audição é normal t0 - t =0. Logo P. A.= x 0 ou P. A. O. Isto é para o diapasão 128 d. v.

Repetindo-se a manobra numerica obtem-se os mesmos resultados.

Logo, o diapasão, como o audiometro, parte do limiar de audibilidade isto é no nivel zero da ficha (W. E. - 6A).

Ajustaremos, agora, a curva de surdez total (em segundos) sobre a respectiva curva (expressa em decibel) do audiometro.

P. A.= (tº - t), logo. P. A./A = t9 - t

Para o diapasão 128 d.. v. do audiometro (Vide ficha) a surdez total é igual a 94 decibels

pois 94/1,08 = 87

87 é a surdez maxima para o diapasão 128 d. v .

Em seguida, identicamente, obtem-se a surdez maxima respectivamente para cada diapasão:

Frequencia - 128 - 256 - 512 - 1024 - 2048
Audiometro - 94 - 105 - 115 - 120 - 120 - decibels
Diapasão- 87 - 77 - 88 -72 -56 - segundos

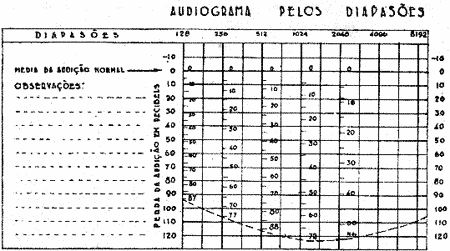
Determinadas as duas linhas extremas do campo auditivo resta dividir em partes iguais cada coluna vertical:

Para o 128 - de O ......87 segundos
Para o 256 - de O ......77 segundos
Para o 512 - de O ......88 segundos
Para o 1024 - de O ......72 segundos
Para o 2048 - de O ......56 segundos

Fig. 6 - Neste grafico observa-se a diferencial acustica entre a audição do paciente e a do examinador, isto é, o espaço representado por Y.

APLICAÇÕES CLINICAS DO DIAGRAMA

Mede-se com os diapasões, em segundos de audibilidade, a condução aerea e ossea do paciente, para cada frequencia, e comparar respectivamente com a do examinador considerada normal.

Quando o paciente deixar de ouvir o diapasão, o medico aproxima-os ao seu ouvido.

O excesso ele audição ouvido pelo medico (diferencial acustical) é registrada no diagrama.

É intuitivo que para a condução ossea registra-se a prova de Schwabach.

Lamentavelmente até o presente não conseguimos obter a constante do diapasão 4096 d. v. (c,), constituindo assim uma lacuna evidente no diagrama.

Este metodo está dentro dos 3 itens enunciados.

É simples, é eficaz e é função, da constante de amortecimento de cada diapasão.

Alem disso pode ser construido por qualquer serie de diapasões desde que sejam calibrados e dos quais se conheçam as suas constantes de amortecimentos.

Póde ainda ser utilizada qualquer ficha audiometrica como por exemplo: a do Sonotone.
No caso particular da tabela deste aparelho, o grafico ainda será mais facil.

Outra vantagens deste metodo é o registro da diferencial acustica eliminando, de certo modo, a percussão inicial uniforme, a qual, nem sempre é facil de se conseguir.

BIBLIOGRAFIA

FLETCHER H. - Speech and hearing - von Nostrand 1919.
STUDIES OF THE VIII NERVE - THe Laringoscope Press - 1939.
W. THOMAS AND YATES - Principles and pratic ofotology. BALTIMORE - Wood & Company - 1933.
AARON ROTH - Tuning forks auiliun,tcr. Archives of otology Vol. 31 - 1940.
FOWLER - Loose leaf - Medicine.
JOHNSON F. A. H. - Interpretation of results of tuning forks test for deafness. Arch of otolaringology - Vol. 27 - 1938.
REZENDE BARBOSA - Alguns dados de aplicação pratica na acumetria. Revista Brasil de otorinolaringologia - Vol. 7 - 1939.
BEST and TAYLOR - Physiological basis of medicar pratico - 2.ª edição - 1939.

SUMMARY

Tuning Fork audiogram

The diagram is a duplicate of the Western Electric 6A model. The vertical lines corresponding to the tuning forks frequencies figures indicating the hearing loss in seconds are added. The distribution of these figures were obtained through Fletcher's equation:

H. L. = (tº-t)

The difference in seconds between the patienfs hearing and that of the examiner is registered on the vertical lines ad thus the audiogram is obtained (see chart).

Imprimir: